The intimately related topics of atomic structure and chemical bonding are universally regarded as the 'heart of Chemistry'; not surprisingly, therefore, one's knowledge of these topics and this science increase in parallel. Rather encouragingly, a student and a mature scientist share similar mental images of both atomic and molecular structure, as can be illustrated using a common point of reference; thus, ...

Although neither of these mental images has the slightest relationship either to physical reality or to their respective analogies, they do provide a quite convenient starting point from which ever-increasingly detailed 'pictures' can be drawn ...

The following flow diagram shows a possible pathway to a comprehensive understanding of either of these two topics: Mental image (student and mature scientist) ———® Sketch 1 (student) ———® Sketch 2 ——® Finished drawing ———® Water color ———® Oil painting (? ... mature scientist).

Ideally, a student needs to acquire sufficient knowledge, on the one hand, to be able to draw Sketch 1, and on the other, which will allow Sketch 2 to be drawn (at a later date) using an eraser and a pencil — without the need to discard Sketch 1 for a new piece of paper.

For decades, the received wisdom has been that Sketch 1 should be drawn using theories formulated in the 1910s. In particular, these involve viewing the electron purely as a particle; and, in terms of presenting an introduction which is easier to understand, this restrictive view has undoubted advantages. Nevertheless, the properties of an electron are consistent with its dual behavior as a particle and a wave. The evidence for, and acceptance of, this duality forms the basis of Sketch 2 (and with it comes a spectacular increase in one's understanding of Chemistry).

In this introduction, apart from one mischievous exception, no attempt has been made to draw Sketch 1 using contemporary theories. However, a robust framework is presented which is consistent with two unifying concepts that have remained unchanged with the advances in theoretical knowledge: first, electrons occupy either atomic or molecular energy levels; and second, chemical bonding occurs because the resulting molecule or compound has a lower energy than its constituent atoms.

Furthermore, because the limitations of Sketch 1 are stated, and the necessary simplifications are kept to a minimum, it should be possible to draw Sketch 2 using the same piece of paper.


Energy Levels ... Precepts
Each diagram in Figures (a-h) show an infinite number of steps, each 1.0 m in height, and a 1.0 kg ball which is either occupying a step or being transferred from one step to another; each step may be correctly and usefully viewed as an energy level.

Figures (a-h)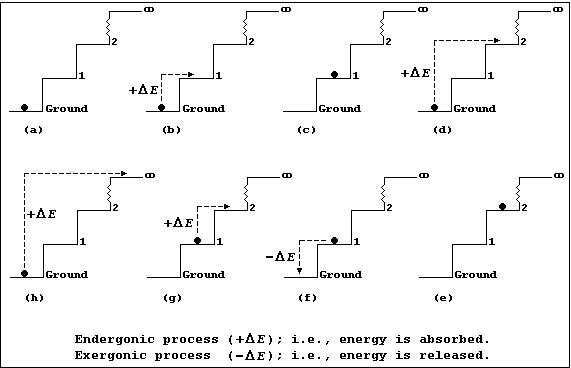

Figure (a) shows a 1 kg ball occupying the ground step; all the other steps are unoccupied. The energy (E) of the 1.0 kg ball is 0 kJ (i.e., E = m × g × h = 1.0 × 10 × 0.0 = 0 kJ).

Figures (b) and (d) show, respectively, the ball being transferred from the ground to the 1st step and from the ground to the 2nd step; each process is endergonic (+DE); i.e., energy is absorbed (for example, by transducing chemical or mechanical energy to potential energy, via kinetic energy).

Figures (c) and (e) show, respectively, the ball now occupying the 1st and 2nd steps; it has acquired 10 kJ of potential energy on the 1st step [Figure (c)] and 20 kJ on the 2nd step [Figure (e)].

Figure (f) shows the ball being transferred back from the 1st to the ground step: this process is exergonic (-DE); i.e., energy is released (which, typically, may be as heat and sound energy transduced from potential energy, via kinetic energy).

Figure (g) shows the ball being transferred from the 1st to the 2nd step; once transferred it will have acquired another 10 kJ of potential energy. And, obviously, each similar transfer from a lower to a higher step (or energy level) will result in the ball acquiring the additional potential energy.

Figure (h) shows the ball being transferred from the ground step to the (idealized) infinite step, where the Earth's gravitational force will be zero; and, here, the ball will no longer be attracted to the Earth. So, with mischief aforethought, one can say that the hugely endergonic process of transferring the ball from the ground step to infinity, in discrete steps, will result in the ball becoming 'ionized'.

And finally, these precepts hold true: firstly, even when the steps are of non-uniform height (an interesting architectural phenomenon), though the numerical values would be different; and secondly, in both free and bonded atoms, where energy levels of non-uniform height tend to be the rule rather than the exception.


Refreshments ...?
People who are 'positively bursting with the joys of spring' have been known to express a firmly held opinion: namely, that a swim in ice-cold water is refreshing after a hot sauna. Presented below is the chemical equivalent of such a swim: namely, definitions of the commonest terms used in structure and bonding (a few of these have been simplified).

Matter is anything that occupies space and has mass.

A pure substance is a form of matter that has both definite composition and distinct properties.

An element is a pure substance which cannot be broken down into simpler substances by chemical means.

An atom is the smallest particle of an element that can exist and still retain the ordinary chemical properties of that element.

A proton is a sub-atomic particle, within the nucleus of an atom, which has unit mass and unit positive charge.

The atomic number (Z) of an element is the number of protons each atom of that element has in its nucleus; e.g., Z = 17 for chlorine (₁₇Cl).

A neutron is a sub-atomic particle, within the nucleus of an atom, which has unit mass and zero charge.

The mass number (A) of an atom is the number of protons and neutrons it has in its nucleus; e.g., A = 35 for a chlorine atom which contains 18 neutrons (³⁵Cl), and A = 37 for one which contains 20 neutrons (³⁷Cl).

Isotopes are atoms of the same element that contain different numbers of neutrons; e.g., ⁶³Cu and ⁶⁵Cu are two isotopes of copper.

An electron is a sub-atomic particle, outside the nucleus of an atom, which has nearly zero mass and unit negative charge.

An ion is an atom (or group of atoms) which has either gained or lost electrons; e.g., a chloride anion, ₁₇Cl^1-, contains 18 electrons (i.e., one more than neutral atom, ₁₇Cl⁰), and a copper(II) cation, ₂₉Cu²⁺, contains 27 electrons (i.e., two less than the neutral atom, ₂₉Cu⁰).

A compound is a pure substance which contains two or more different elements chemically bonded together in stoichiometric proportions.

A molecule is the smallest part of an element or of a covalently bonded compound that can exist independently and still retain the ordinary chemical properties of that element or compound.

A mixture consists of two or more substances which are not chemically bonded together.

A localized covalent bond describes the mutual electrostatic attraction of two adjacent nuclei for a shared pair of electrons which occupy the same molecular energy level.

A delocalized covalent bond describes the electrostatic attraction of more than two nuclei for a shared pair of electrons which occupy the same molecular energy level.

An ionic bond describes the electrostatic attraction of two oppositely charged ions in a crystalline lattice.

The ground-state electronic structure is the lowest-energy arrangement of the electrons in each free, gaseous, neutral atom of an element.

Each neutral atom of an element consists of a nucleus of Z protons and (A - Z) neutrons, together with Z extra-nuclear electrons; where Z is the atomic number and A is the mass number. The extra-nuclear electrons are arranged in atomic energy levels; the first four of these can hold a maximum of 2, 8, 18, and 32 electrons, respectively. The ground-state electronic structure of an atom is determined by a simple principle: namely, electrons are arranged in such a way that their total energy is a minimum. This Table shows two different methods of representing such electronic structures for all 36 elements in Periods 1 to 4.

		Occupancies of the main energy levels	Occupancies of the sub-levels of the main energy levels (*) (†)
Group	ZAtom	1st 2nd 3rd 4th	1st 2nd 3rd 4th
1	1H	1	1s1
18	2He	2	1s2
1	3Li	2, 1	1s2, 2s1
2	4Be	2, 2	1s2, 2s2
13	5B	2, 3	1s2, 2s2 2p1
14	6C	2, 4	1s2, 2s2 2p2
15	7N	2, 5	1s2, 2s2 2p3
16	8O	2, 6	1s2, 2s2 2p4
17	9F	2, 7	1s2, 2s2 2p5
18	10Ne	2, 8	1s2, 2s2 2p6
1	11Na	2, 8, 1	1s2, 2s2 2p6, 3s1
2	12Mg	2, 8, 2	1s2, 2s2 2p6, 3s2
13	13Al	2, 8, 3	1s2, 2s2 2p6, 3s2 3p1
14	14Si	2, 8, 4	1s2, 2s2 2p6, 3s2 3p2
15	15P	2, 8, 5	1s2, 2s2 2p6, 3s2 3p3
16	16S	2, 8, 6	1s2, 2s2 2p6, 3s2 3p4
17	17Cl	2, 8, 7	1s2, 2s2 2p6, 3s2 3p5
18	18Ar	2, 8, 8	1s2, 2s2 2p6, 3s2 3p6
1	19K	2, 8, 8, 1	1s2, 2s2 2p6, 3s2 3p6 3d0, 4s1
2	20Ca	2, 8, 8, 2	1s2, 2s2 2p6, 3s2 3p6 3d0, 4s2
3	21Sc	2, 8, 9, 2	1s2, 2s2 2p6, 3s2 3p6 3d1, 4s2
4	22Ti	2, 8, 10, 2	1s2, 2s2 2p6, 3s2 3p6 3d2, 4s2
5	23V	2, 8, 11, 2	1s2, 2s2 2p6, 3s2 3p6 3d3, 4s2
6	24Cr	2, 8, 13, 1	1s2, 2s2 2p6, 3s2 3p6 3d5, 4s1
7	25Mn	2, 8, 13, 2	1s2, 2s2 2p6, 3s2 3p6 3d5, 4s2
8	26Fe	2, 8, 14, 2	1s2, 2s2 2p6, 3s2 3p6 3d6, 4s2
9	27Co	2, 8, 15, 2	1s2, 2s2 2p6, 3s2 3p6 3d7, 4s2
10	28Ni	2, 8, 16, 2	1s2, 2s2 2p6, 3s2 3p6 3d8, 4s2
11	29Cu	2, 8, 18, 1	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s1
12	30Zn	2, 8, 18, 2	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2
13	31Ga	2, 8, 18, 3	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2 4p1
14	32Ge	2, 8, 18, 4	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2 4p2
15	33As	2, 8, 18, 5	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2 4p3
16	34Se	2, 8, 18, 6	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2 4p4
17	35Br	2, 8, 18, 7	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2 4p5
18	36Kr	2, 8, 18, 8	1s2, 2s2 2p6, 3s2 3p6 3d10, 4s2 4p6
* The superscripts indicate the number of electrons in each sub-level; for example, 3p5 means that there are 5 electrons in the 3p sub-level. † Introductory courses invariably focus on the occupancies of the main energy levels; so, the student is well advised to view all the entries in this column as exotic species of tasty but unripened pears (... which maybe either plucked at some later date or allowed to rot).

The ground-state electronic structures of gaseous atoms, as summarized by their occupancies of the main energy levels, can be represented by simple electron-structure diagrams (as in the examples shown below).

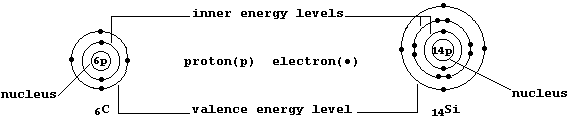
The Table shows the electronic structures of the first 26 elements placed in the so-called main groups (i.e., 1, 2, and 13 to 18). Apart from the single exception of helium, the elements in each group contain the same number of valence (or bonding) electrons in their outermost energy level; in part, it is this periodicity of electronic structures which is the basis of the (modern) Periodic Table of the Elements.

The Table also shows the electronic structures of the first 10 elements placed in Groups 3 to 12. Self-evidently, the occupancies of the two outermost energy levels show no regularity; but, regrettably, there is no simple explanation for the observed anomalies. Nevertheless, three points are worth noting ...

First, scandium (Group 3) behaves as if its electronic structure was effectively 2,8,8,3; and so its chemistry has some similarity to the elements in Group 13.

Second, in contrast to the main group elements, those in Groups 4 to 11, known as the transition elements, have valence electrons in the two outermost energy levels or, more specifically, in the 3d and 4s sub-levels. Because the necessarily detailed descriptions of these sub-levels are (usually) reserved for an advanced course, one's initial understanding of the chemistry of the transition elements will inevitably be quite limited.

And third, zinc (Group 12) has two valence electrons in its outermost energy level; and so its chemistry has some similarity to the elements in Group 2.

Currently, the received wisdom is that emphasis should be given to the correlation of the periodicity of electronic structures with chemical reactivity; an aspect which is readily achieved by limiting studies to elements of Groups 1, 2, 17, and 18. However, many authors have drawn attention to a plethora of caveats [see, for example: F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, Wiley, New York, 1988; and J. E. Huheey, Inorganic Chemistry (Chapter 17), Harper Row, New York, 1983]; just two of these are noted here.

First, Cotton and Wilkinson have written: "Little of the chemistry of silicon can be inferred from that of carbon." A particularly important caveat when one reflects upon two observations: silicon is the second commonest element in the Earth's crust, but carbon forms more compounds than any other element apart from hydrogen. The following 'cluette' may provide some perspective. A student, having compared the occupancies of the main energy levels, would correctly reason that 'carbon and silicon should show similar chemistry because they both have the same number of valence electrons'. Contrastingly, a mature scientist, by drawing upon advanced theoretical models, would reason that 'their chemistry should differ because of the different characteristics of their occupied and unoccupied sub-levels'. Thus, the two individuals will be perceiving electronic structures (and the Periodic Table) in very different ways.

And second, elements in a group do not always form ions with the same charge; e.g., in Group 11, the commonest ions of copper, silver, and gold are, respectively, Cu(II), Ag(I), and Au(III) — admittedly, these are transition metals: but then so are over half of all those known.

Bonding between atoms, which occurs because the resulting molecule or compound has a lower energy than its constituent atoms, is achieved by redistributing the valence (or bonding) electrons. In covalent bonding, this redistribution occurs by the atoms sharing two or more electrons.

The term localized covalent bond describes the mutual electrostatic attraction of two adjacent nuclei for a shared pair of electrons which occupy the same molecular energy level.


The Mechanism of Covalent Bonding
Consider two hydrogen atoms, Ha and Hb. The (potential) energy of each electron, in its own separate atomic energy level, is reduced when both electrons enter a molecular energy level which encompasses both nuclei; in doing so, and forming a localized covalent bond, potential energy is transduced to heat energy. So, bond formation is an exothermic process:

Ha(g) + Hb(g) ——————————® H—H(g) DH = -432 kJ mol-¹ *

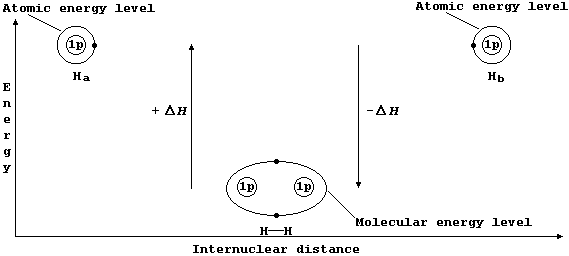
* Conversely, bond breaking, as in the dissociation of dihydrogen, is an endothermic process:

H—H(g) ——————————® Ha(g) + Hb(g) DH = +432 kJ mol-¹

Localized Single Bonds
The sketch graph above includes a method of representing the electronic structure of dihydrogen which is a fairly reasonable approximation to physical reality; in particular, it emphasizes that — after bonding — the two electrons are indistinguishable from one another and that they occupy one molecular energy level (not separate atomic energy levels).

However, similar representations for more complex molecules are rarely used because the resulting diagrams are inevitably more complicated.

Shown below, for dihydrogen, is the simplest type of electron-structure diagram.

The merits of this type of electron-structure diagram are two-fold. First, the retention of the atomic energy levels simplifies 'electronic book-keeping'. And second, there is a clear and direct relationship to one standard method of representing a molecule: i.e., by its structural formula.

Shown below are electron-structure diagrams for atomic fluorine and molecular fluorine (or difluorine).

A fluorine atom contains seven electrons in its outermost atomic energy level; because one of these is unpaired, such an atom is known as a free-radical. The potential energy of this unpaired electron is reduced when it becomes part of a covalent bond; as occurs, for example, when a molecule of difluorine is formed.

The covalent bond in difluorine is formed in the same manner as that in dihydrogen. Thus, one electron from the outermost atomic energy level of each fluorine atom enters a molecular energy level which encompasses both nuclei; the other (non-bonding) electrons form lone-pairs.

Difluorine is an example of a molecule which conforms to the so-called 'octet rule'; i.e., an atom — other than H, He, Li, Be, or B — tends to form bonds until it is surrounded by eight valence electrons. [This is a useful rule of thumb for the electronic structures of molecules which contain only carbon, nitrogen, oxygen, or fluorine. Nevertheless, there are innumerable examples of compounds which contain bonded atoms that have either an 'incomplete' or an 'expanded' octet.*]

Shown below are electron-structure diagrams for hydrogen fluoride and water.

Because the bonds in these two molecules are formed in the same manner, and for the same reason, as both dihydrogen and difluorine, one might expect no further comment. But, together, these four molecules beg an important question: are all covalent bonds the same? The short answer is no! However, in an introductory text, quite how much detail should accompany this flat answer is difficult to judge; and so, rather than throwing caution to the winds, only three brief points are made here.

First, by analogy with the different energy levels observed in atoms, one would expect there to be different molecular energy levels. Indeed, although well beyond the scope of this text, both spectroscopic studies and theoretical calculations provide support for such an expectation; e.g., the molecular energy levels associated with the covalent bonds in H-H, F-F, H-F, and H-O-H are all different.

Second, perhaps intuitively, one might expect that the electrons are not equally distributed when the two nuclei are different; the unequal distribution of 'electron density' is known as polarization (and occurs in both H-F and H-O-H, for example: but not in either H-H or F-F).

And third, quantitative determinations of molecular energy levels and polarization, amongst other bonding parameters, allow many reactions of molecules to be both correlated and predicted.

* As a caveat to the 'octet rule', consider the following. Each of the 46 chromosomes present in (most) cells of the human body contain bonded phosphorus which does not adopt the electronic structure of argon. [... And setting aside identical sprogs, the exponentially increasing human population is? ... And setting aside the depressing fact that numbers are ever decreasing, because of pollution, the number of species is?]

Multiple bonding will occur between atoms if the resulting molecule or compound has a lower energy than that achieved by single bonding. [No attempt will be made here to explain (in detail) the reasons why some pairs of atoms have little or no tendency to form multiple bonds; e.g., in contrast to the vast numbers of compounds which contain C=C bonds, those with Si=Si bonds are very rare indeed.]


Localized Double Bonds
Shown below are electron-structure diagrams for ethane and ethene.

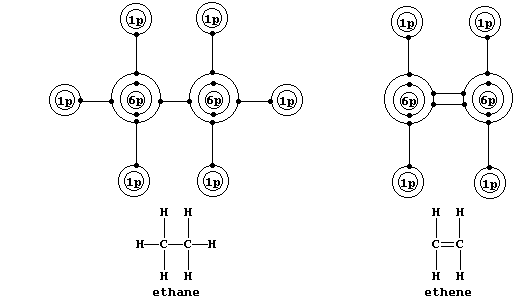
Ethene contains what is (universally) known as a double bond. However, perhaps contrary to one's initial expectations, these two bonds are not identical: one of these, known as a s (sigma) bond, consists of two electrons at one molecular energy level; and the other, known as a p (pi) bond, consists of two electrons at another molecular energy level.

These equations summarize the partial dissociation of ethene (Eq. 1) and the complete dissociation of ethene (Eq. 2) and ethane (Eq. 3):

Eq. 1 H₂C=CH₂ —————————® H₂C-CH₂ DH = +264 kJ mol-¹
Eq. 2 H₂C=CH₂ ——————————® H₂C + CH₂ DH = +610 kJ mol-¹
Eq. 3 H₃C-CH₃ ——————————® H₃C + CH₃ DH = +346 kJ mol-¹

Equations 2 and 3 show that the double bond is stronger than the single bond by 264 kJ mol-¹; and Equations 1 and 3 show that the p bond is weaker than the s bond by 82 kJ mol-¹. Despite the increased strength imparted by double bonding, ethene is more reactive than ethane; e.g., in the absence of light, bromine reacts with ethene but not ethane.*

A partial explanation for this apparent anomaly is as follows: both molecules contain a s bond between the carbons, but bromine reacts with the (localised) p bond present only in ethene.

* Demonstrating the differences in chemical reactivity between ethane and ethene is cumbrous, because both are gases at r.t.p.; the simplest homologs of the alkanes (C_nH_2n+2) and alkenes (C_nH_2n) which are not either gases or highly volatile liquids, and which can be investigated safely and conveniently, are hexane and hex-1-ene, respectively.


Localized Triple Bonds
Shown below are electron-structure diagrams for ethyne, dinitrogen, and carbon monoxide.

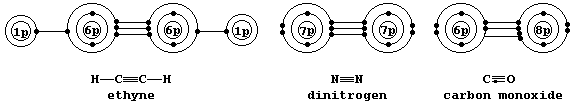
Each of these molecules contains what is known as a triple bond; i.e., one s bond and two p bonds (p1 and p2), with each bond consisting of two electrons in different molecular energy levels that encompass the nuclei of the principal atoms (i.e., C, N, and O). Although each bonded principal atom contains an octet of electrons, the different manner by which this is achieved in carbon monoxide merits describing the bonding in detail. Setting aside each lone-pair, localized about its respective nucleus, a description of the triple bonding in carbon monoxide is as follows: one s bond, containing one electron from each atom; one p bond (p1), containing one electron from each atom; and another p bond (p2), containing two electrons from the oxygen atom.

	Nominal bond energy of each bond / kJ mol-¹			Total bond energy / kJ mol-¹
	s	p1	p2	S s + p1 + p2
Ethyne (HCºCH)	346	264	205	815
Dinitrogen (NºN)	167	251	528	946
Carbon monoxide (CºO)	360	385	324	1069

The above Table reveals that each of these triple bonds is very strong but that the strength of each component varies within and between the three molecules. Their (relative) difficulty of reduction by dihydrogen is NºN >> CºO > HCºCH; an order that parallels the energy of the p2 bond (NºN >> CºO > HCºHC), but not the total bond energy (CºO > NºN > HCºCH). This correlation may just be coincidental, however; certainly, other bonding parameters, including molecular energy levels and polarization, are known to influence the rate of reaction. [Here, for example, it is noteworthy that dinitrogen is non-polar, whereas carbon monoxide and ethyne are both polar molecules (with an unequal distribution of 'electron density' about the nuclei).]

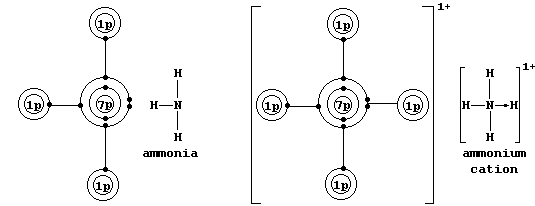
* A covalent bond in which one of the atoms donates both electrons is called either a coordinate or a dative bond; such bonds are often, but not always, represented by an arrow showing the direction of donation. Coordinate bonding is very common (particularly so in compounds of the transition elements); one example is an ammonium ion, in which nitrogen uses its lone-pair to form a coordinate bond with a hydrogen ion.

Bonding between atoms, which occurs because the resulting molecule or compound has a lower energy than its constituent atoms, is achieved by redistributing the valence (or bonding) electrons. In ionic bonding, this redistribution occurs by the atoms transferring one or more electrons.

The term ionic bond describes the electrostatic attraction of two oppositely charged ions in a crystalline lattice.


The Mechanism of Ionic Bonding
Formally, the ionic compound sodium fluoride — which contains Na¹⁺ and F^1- ions, each with an octet of electrons — results from the transfer of one valence electron from a sodium atom to a fluorine atom; i.e.,

Na atom + F atom ——————————® Na1+ion + F1-ion  2,8,1     2,7                  2,8     2,8

Despite the attractiveness of such a simple summary, one needs to peer into the mechanism of ionic bonding in order to prevent misconceptions.

The formation of solid sodium fluoride, NaF(s), from solid sodium and gaseous difluorine, can be divided into five ergonic processes; i.e.,

Na(s) —————————————————————® Na(g)   DH1 Na(g) —————————————————————® Na1+(g) + 1e-   DH2 F2(g) —————————————————————® 2F(g)   DH3 F(g) + 1e- ————————————————® F1-(g)   DH4 Na1+(g) + F1-(g) ———————————® Na1+(s)F1-(s)   DHL

Experiments show that formation of these gaseous ions is endothermic; i.e., SDH_I, the value of DH₁ + DH₂ + DH₃ + DH₄, is positive. In sharp contrast, formation of the solid from these gaseous ions is exothermic; i.e., the value of DH_L, known as the lattice energy, is negative. Solid sodium fluoride forms because the value of DH, DH_L - SDH_I, is negative; so, the 'driving force behind' the formation of sodium fluoride is the overwhelmimg exothermicity of the attractions of the oppositely charged ions for each other (... and not the formation of ions with an octet).

Furthermore, because experiments have shown that, for every combination of metallic and non-metallic element, the corresponding value of SDH_I is positive, the formation of an ionic compound is determined largely by the value of DH_L (the lattice energy).

This ('long-winded') approach above allows a qualitative understanding of some apparent anomalies; two illustrative examples are given here.

Firstly, Na₂O, MgO, Al₂O₃, NaCl, and MgCl₂ are all ionic compounds in which the ions have an octet: but, although aluminum and chlorine can readily form ions with an octet, aluminum chloride is a covalent compound. The explanation is as follows: DH_L - SDH_I is negative in each of the first five compounds, but DH_L - SDH_I is positive for the hypothetical ionic compound Al³⁺(s)3Cl^1-(s)

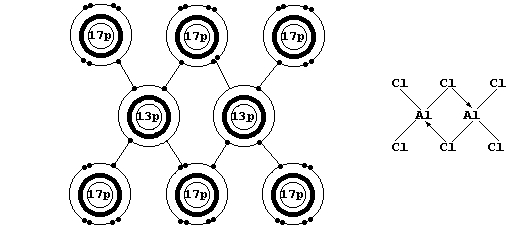
[When gaseous aluminum chloride is cooled, discrete AlCl₃ molecules dimerize to form Al₂Cl₆ (see the electron-structure diagram above).]

And secondly, NaCl and MgCl₂ are both ionic compounds in which the ions have an octet: but, although transition elements do not form ions with an octet, CuCl₂ and FeCl₂ are also ionic. The explanation is as before; thus, DH_L - SDH_I is negative in each of these four compounds.

In the absence of either experimental or calculated data, the student will ask (or even demand) to know how one predicts the type of bonding in any given compound. Although there is no predictive method which is foolproof, two rules of thumb are useful: first, the bonding between non-metallic elements is normally covalent; and second, the bonding between metallic and non-metallic elements is commonly ionic.*

[* In point of fact, the exceptions to this rule of thumb are legion. However, such exceptions usually make no more than 'guest appearances' in an introductory course (... a rare case of 'ignorance is bliss' ?).]


The Structures and Physical Properties of Ionic Compounds
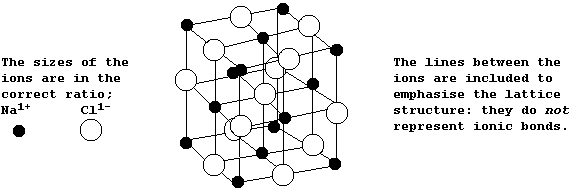
The diagram below shows the structure of NaCl; the oppositely charged ions are arranged in a symmetrical pattern within a crystal lattice.

The electrostatic attractions between the oppositely charged ions in the crystal lattices of ionic compounds are strong and omnidirectional: and so, such compounds show several characteristic physical properties; however, only three of these will be considered here.

First, they tend to have high melting points; a large amount of thermal energy must be supplied to the crystal lattice before the ions vibrate vigorously enough to overcome the electrostatic forces of attraction.

Second, they do not conduct electricity in the solid state, because there are no free-moving ions to carry the current: contrastingly, they do conduct electricity in either the liquid state or when dissolved in water, because the ions are free to move.

And third, they tend to be insoluble in organic solvents and soluble in water; the hydration energy released when ions are dissolved in water is often similar to or greater than the lattice energy.

Not surprisingly, these characteristic physical properties are used as evidence for ionic bonding: but there are at least three caveats.

First, high melting points are also observed for covalent substances with giant structures [e.g., carbon-graphite and silicon(IV) oxide].#

Second, the measurement of electrical conductivity can be precluded because the compound either thermally decomposes before melting or has a low solubility in water [e.g., many carbonates and nitrates decompose before melting, and most oxides and sulfides are insoluble in water].

And third, a wide variety of covalent compounds are also soluble in water [e.g., many alcohols and carbohydrates with small molar masses].

# Typically, covalent substances with simple molecular structures have low melting points, because the attractive forces between molecules are weak, are insulators of electricity, because there are no free-moving ions, and are soluble in organic solvents such as trichloroethane.

An element (E) is defined as 'a pure substance which cannot be broken down into simpler substances by chemical means'. Of the 111 elements so far characterized, 81 are stable (H ... Mo, Ru ... Nd, and Sm ... Bi), whereas 30 occur only as radioactive isotopes (Tc, Pm, and Po ... Uuu); extensive compilations of various data for most elements are included in reference books (e.g., The Handbook of Physics and Chemistry).

This first Table shows selected data for 13 of the 81 stable elements, including those for the best electrical conductor (silver).

	CE / MW cm-¹	CT / W m-¹ K-¹	TM / K	TB / K	r g cm-³	DH1 / kJ mol-¹	DH2 / kJ mol-¹
Ag	68.0	428	1235	2433	10.5	289	731
Cu	64.5	403	1356	2853	8.9	339	745
Au	48.8	319	1337	3080	19.3	369	890
Al	40.0	236	933	2623	2.7	314	578
Mg	25.4	157	922	1363	1.7	150	938
Na	23.8	142	371	1173	0.97	109	496
In	12.5	84	430	2323	7.3	244	558
Pt	10.2	72	1995	3993	21.5	565	868
Ga	7.4	41	302	2342	5.9	289	579
As	3.8	39	886-subl.		5.7	290	946
Hg	1.1	8	234	630	13.6	61	1007
Mn	0.7	8	1517	2393	7.4	279	717
Te	0.001	-	723	1263	6.3	199	869
Electrical conductivity (CE); Thermal conductivity (CT); Melting point (TM); Boiling point (TB); Density (r) at 293 K. Heat of sublimation (DH1), defined as the energy required to separate a gaseous atom from the solid element; i.e., E(s) —® E(g). First ionization energy (DH2), defined as the energy required to remove one electron from an isolated gaseous atom; i.e., E(g) —® E1+(g) + 1e-. Conductivity values refer to data obtained at ambient temperatures (288 - 298 K).

These compilations show that no element has an electrical conductivity between 0.001 MW cm-¹ (Te) and 0.7 MW cm-¹ (Mn), and so a metallic element can be precisely defined as 'a pure substance which cannot be broken down into simpler substances by chemical means, and which has an electrical conductivity greater than or equal to 0.7 MW cm-¹ at ambient temperatures'. This definition may appear unduly pedantic, but its use results in 62 of the 81 stable elements being classified as metallic and 19 as non-metallic (H, He, B, C, N, O, F, Ne, Si, P, S, Cl, Ar, Se, Br, Kr, Te, I, and Xe). Furthermore, this definition tacitly recognizes the occurrence of elements whose conductivities are increased either by photo- or thermal-excitation or by the presence of trace impurities (e.g., 'semi-conductors' such as silicon), as well as those which show 'superconductivity' at very low temperatures (e.g., hydrogen).

Three initial problems arise when attempting to introduce an overview of metallic elements. First, they do show typical properties, such as high electrical and thermal conductivities, high melting and boiling points, and high densities: but there are several anomalies which are difficult to explain; e.g., the melting points of cesium, gallium, mercury, potassium, rubidium, and sodium are all lower than several non-metallic elements. Second, there is a reasonably acceptable linear relationship between electrical and thermal conductivities (i.e., C_E » k × C_T + c): but, as is clearly apparent from inspection of those data in the above Table, there are no correlations between any other pair of physical quantities. And third, their typical properties are invariably attributed to metallic bonding: but simple descriptions of this phenomenon, which are not misleading, have proven elusive ...

The following description of a metal, or minor variants thereof, has been commonly included in introductory texts: 'a metal consists of a lattice of positive ions embedded in a sea of electrons'. However, for at least three reasons, this description must be firmly eschewed.

First, the term 'lattice' refers strictly to the solid state: but, as evinced by conductivity data (see, for examples, those shown in this second Table), metallic bonding clearly persists in the liquid state.

	Hg	Cs	Ga	Rb	K	Na
Conductivity at 293 K / MW cm-¹	1.0	5.0	7.5	8.0	16.5	24.0
Melting point / K	234	301	303	312	336	371
Conductivity at 373 K / MW cm-¹	1.0	2.0	3.5	3.5	5.5	10.5

Second, researchers do not invoke 'ionization' in their descriptions of metals; the experimental data, together with theoretical calculations, support a bonding model which is fundamentally covalent in character.*

And third, 'a sea of electrons' is a peculiarly mixed metaphor; thus, conduction in aqueous solutions occurs via free-moving ions, whereas conduction in metals occurs via free-moving delocalized electrons.#

Quite reasonably, one would expect, as a minimum, a description of the bonding in metallic elements to provide at least partial explanations for two observations: first, the 100-fold difference in electrical conductivity between silver and manganese; and second, the 700-fold difference in electrical conductivity between manganese and tellurium. Unfortunately, however, such expectations probably cannot be realized from a simple qualitative description of metallic bonding. Furthermore, there may not be such a description which is illuminating without being misleading: so the following attempt may only score marks 'for effort'.

'A metal consists of a giant covalent structure, in which each atom has contributed one or more of its valence electrons to the formation of omnidirectional, delocalized covalent bonds that extend throughout the structure.' §

Strictly speaking, this description of a metal does not 'explain' its characteristic properties: but advanced theories of metallic bonding indicate that it is concordant. In particular, it is consistent with two platitudes: 'a metal is a good conductor of electricity because of the presence of free-moving delocalized electrons', and 'a non-metal is a poor conductor of electricity because of the absence of free-moving delocalized electrons'.

* See, for example, R. Hoffmann, Solids and Surfaces, VCH Publishers, New York, 1988 (and references cited therein).
# An extended critique of this description would be inappropriate here and, indeed, unnecessary because a beautifully balanced summary of both historical and contemporary bonding theories in metals has been written by J. D. Lee [Concise Inorganic Chemistry (pp. 114 - 118), Harper Row, London, 1991]. However, the student is invited to consider constructing and testing various hypotheses, using the electrical conductivity, heat of sublimation, and first ionization data shown in the first Table.
§ The following notes should provide a slightly deeper perspective ... Each sodium atom has one electron in its outermost atomic energy level: so 1 mole of sodium metal contains 6.022 × 10²³ valence electrons which contribute to the formation of covalent bonds. A covalent bond contains two electrons which occupy the same molecular energy level: so 1 mole of electrons contains half this number of covalent bonds. In principle, each of these (very closely spaced) levels encompasses the 6.022 × 10²³ nuclei: so there are 3.011 × 10²³ omnidirectional, delocalized covalent bonds extending throughout 1 mole of sodium metal.

Chemistry texts are often peppered with statements of the following type: 'potassium is a strong reducing agent'; 'calcium is a stronger reducing agent than magnesium'; 'acidified potassium manganate is a strong oxidizing agent'; and, 'fluorine is a stronger oxidizing agent than chlorine'. The quantitative basis for these and other related descriptions is the (continually expanding) set of physical quantities known as reduction potentials; a critical compilation of these data is: A. J. Bard et al., Standard Potentials in Aqueous Solution, Marcel Dekker, New York, 1985. Numerical values of redox potentials are rarely used in introductory courses, partly because their correct use is quite complicated: nevertheless, a selected sub-set of values — as shown in this first Table — does provide a useful point of reference. [Reductant and reducing agent are synonymous, as are oxidant and oxidizing agent.]

These data have been obtained, under standardized conditions, using sophisticated electrochemical cells. The diagram shows the basic design of such cells; Cell 1 would be suitable for impoverished mortals, but the well-endowed (or alchemists) would surely prefer Cell 2.

Chemically, a metallic element (M) is characterized by its tendency to lose one or more electrons and form a positive ion; i.e., it is readily oxidized (Olé !): M ——————® Mⁿ⁺ + ne^-. One of several different methods of quantitatively comparing metallic character involves using oxidation potentials. In principle, these values can be determined by measuring potential differences of simple electrochemical cells. However, because published sources of reduction potentials contain data obtained under standardized conditions, it is both convenient and self-consistent to derive oxidation potentials from such sources. This derivation involved changing the sign of each value, assigning an arbitrary value of 0.00 V to a gold reference electrode, and then executing simple arithmetic; these data were obtained under standard conditions (pH = 0; 298 K).

An element's metallic character can be precisely defined in terms of electrical conductivity, as exemplified by the sub-set shown below:

[Ag > Cu > Al > Ca > Mg > Na > Zn > K > Fe > Sn > Pb > Hg]

However, an element's metallic character is more usually considered in terms of chemical reactivity; and, as exemplified by the same sub-set, there is no apparent correlation between conductivity and reactivity:

[K > Ca > Na > Mg > Al > Zn > Fe > Sn > Pb > Cu > Hg > Ag]

There is just the 'small' matter of defining chemical reactivity ...


Bon gré, mal gré?
The addition of a small quantity of solid potassium to water results in the molten metal whizzing over the water's surface and the evolved gas catching fire with a lilac flame. By contrast, a similar experiment with solid lithium merely results in steady evolution of the gas (dihydrogen).

[Scene. A (kangaroo?) court in the state capital of Laputa.] Prosecutor: M'Lud. These results prove, beyond any reasonable doubt, that Mr. Potassium is more reactive than the defendant. Judge: Thank you kindly, Sir. [He addresses the prosecutor.] A splendid case for the prosecution, if I may so say. Has the defendant anything to add before I pass sentence? Mr. Lithium: Yes, my Lord. I do admit that I have a higher activation energy: but, my reaction with water is more exothermic than Mr. Potassium's. Judge: Stop! This Court will not be blinded by science ... Mr. Lithium: But ... Judge: Silence! You are in contempt of this Court. [He places a black handkerchief over his grubby-looking, moth-eaten wig.] Mr. Lithium, I sentence you, for the rest of your natural life, to a position below Mr. Potassium in the Reactivity Series. [Cheers from the public gallery.]

The explanation for the observations above is as follows. Potassium has a low melting point, 63°C, and so the heat of reaction is sufficient to make it melt; the molten metal spreads out to expose a larger surface area, and so it reacts even faster: as a result, heating in situ causes the dihydrogen gas to catch fire. By contrast, lithium reacts much more slowly, because it has a higher melting point, 181°C, and so there are fewer collisions between the particles; its reaction with water is more exothermic, but this heat energy is released more slowly. These energy level diagrams provide an alternative summary of this explanation.

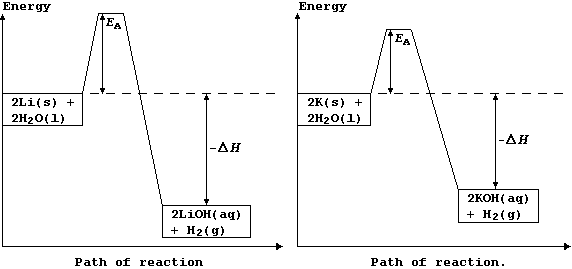
[Scene. The re-trial in the same (kangaroo?) court of Laputa.] Counsel: M'Lud. These energy level diagrams are important new evidence; they prove, beyond any reasonable doubt, that my client is more reactive than Mr. Potassium. Judge: Thank you most kindly, Sir. [He addresses counsel.] I am obliged to say that you have presented a waterproof case for the defense. [The legal beavers humor the judge by smiling weakly.] A clear miscarriage of justice. Has the defendant anything to add before I overturn the original verdict? Mr. Lithium: Indeed I do, my Lord. In contrast to Mr. Potassium, I react readily with dinitrogen. Nevertheless, with most other reactants, I am less ... Judge: Please do stop! Time, or at least my time, is valuable. [He glances briefly, but wistfully, at his golf clubs.] This Court will not be blinded by yet more science ... Mr. Lithium: But ... Judge: Silence! You are in contempt of this Court. [He places a white handkerchief over his (now) grubbier-looking, moth-eaten wig.] Mr. Lithium, I place you in a position above Mr. Potassium in the Reactivity Series. [Cheers from the (clearly undiscriminating) public gallery.]

Indirectly, the reactions of lithium and potassium 'crystallize' two problems which bedevil chemists, whether they be putative or mature. First, the almost irresistible tendency to blur the distinction between the rate and the energy change of a reaction. This blurring appears to establish strong roots at an early stage in one's scientific career: so much so, that authors of university and specialist textbooks invariably feel the need to remind their readers of the distinction.* And second, perhaps in the desire 'to hammer the subject into shape', a tendency to assume that a limited number of reactions will necessarily establish a rule which can be applied willy-nilly (bon gré, mal gré).

Neither of these problems are likely to disappear in the near future: but their adverse effects can certainly be minimized by bearing in mind four principles.

First, there is no connection between the activation energy and the heat energy change (DH) for a chemical reaction.

Second, to ensure consistency, chemical reactivities should be compared only in terms of energy (DE) or heat energy (DH) changes.#

Third, despite inevitable limitations in its use, a (metal) reactivity series based on standard redox potentials is inherently self-consistent because it is derived from measured physical data.

And fourth, a metal (M) reactivity series, based on redox potentials in aqueous solutions, and a Periodic Table of the Elements, which is just a method of summarizing the ground-state electronic structures of gaseous atoms, both provide a suitable focus for correlation: but, neither should be considered as a substitute for experimental facts.

* See, for example, F. A. Cotton and G. Wilkinson, Advanced Inorganic Chemistry, Wiley, New York, 1988; P. W. Atkins, Physical Chemistry, Oxford University Press, Oxford, 1989; and, P. J. Sykes, A Guidebook to Mechanism in Organic Chemistry, Longman, London, 1986.
# Acceptance of this principle does not preclude comparing the rates of reactions. [In advanced studies, reactivities are compared in terms of kinetic and thermodynamic stabilities, which are discussed in terms of activation energies and free energy changes (DG), respectively.]

A healthily critical attitude to reactivity can be acquired from the careful consideration of the following example of hypothesis testing.

[Li > K > Ca > Na > Mg > Al > Zn > Fe > Sn > Pb > (H) > Cu > Hg > Ag]

Quelle horreur!
Hypothesis: 'Within each group of the Periodic Table, the reactivities of the metallic elements (M) increase with increasing atomic number.'
Data: A. J. Bard et al., Standard Potentials in Aqueous Solutions, Marcel Dekker, New York, 1985.
Results: Standard oxidation potentials derived from this source of data show that the ease of oxidation for the metallic elements of six groups is as follows.
Group 1: ₃Li > ₃₇Rb ³ ₁₉K ³ ₅₅Cs > ₁₁Na
Group 2: ₅₆Ba > ₃₈Sr > ₂₀Ca > ₁₂Mg > ₄Be
Group 3: ₅₇La > ₃₉Y > ₂₁Sc
Group 11: ₂₉Cu > ₄₇Ag > ₇₉Au
Group 12: ₃₀Zn > ₄₈Cd > ₈₀Hg
Group 13: ₁₃Al > ₃₁Ga > ₄₉In > ₆₁Tl
Sources of Error: Surprisingly, reference books reveal a wide variation in the numerical values of redox potentials. Nevertheless, in terms of the ordering within groups, such books are concordant with Bard et al.
Conclusion: As adjudged by standard oxidation potentials, in a study limited to the elements in Periods 2 to 6, the data provide no general support for the hypothesis. Thus, Group 1 is irregular; the ease of oxidation does increase as the atomic number increases in both Groups 2 and 3 (i.e., as each group is descended): but, the ease of oxidation decreases as the atomic number increases in Groups 11, 12, and 13. However, the use of different criteria for reactivity may well provide support for this hypothesis.*

After due consideration of the above example of hypothesis testing, a student may well exclaim: "Quelle horreur! Is there no method to this madness?" The answer is yes: if, and only if, one accepts that many patterns in Chemistry are complex, and that they start to emerge only after focusing closely on the details.


Plus horreur?
A preliminary insight into some of the variables which determine the reactivity of metals can be gained by placing a specific reaction type 'under the microscope'; e.g., reaction of a solid metal with an aqueous solution of acid to form a hydrated metal cation and dihydrogen gas:

M(s) + H¹⁺(aq) ———————————® M¹⁺(aq) + ½H₂(g)

This reaction can be divided into several ergonic processes; the Table below shows typical values of these processes for four metals known to form uni-positive cations.

Ergonic process / kJ mol-1	Li	K	Na	Ag
M(s) ———————————® M(g) DH1	161	90	109	289
M(g) ———————————® M1+(g) + e- DH2	520	419	496	731
M1+(g) ——————————® M1+(aq) DHH	-523	-331	-419	-464
H1+(aq) + e- ————® ½H2(g) DHR	-432	-432	-432	-432
M(s) + H1+(aq) ——® M1+(aq) + ½H2(g) DH	-274	-254	-246	+124
DH = DHS + DH1 + DH2 + DHR, where: DH1 is the heat of sublimation; DH2 is the 1st ionization energy; DHH is the heat of hydration of the metal cation; and, DHR is the heat of reduction of the aqueous hydrogen ion to molecular dihydrogen.

A complete explanation of these tabulated data is well beyond the scope of this text: but even a partial explanation should be illuminating ...

Two processes are always endothermic, the heat of sublimation (DH₁) and the 1st ionization energy (DH₂), whereas two are always exothermic, the heat of hydration of the metal cation (DH_H) and the heat of reduction of the aqueous hydrogen ion to molecular dihydrogen (DH_R). Because the value of DH_R is constant, the differences in the overall heat energy change (DH) depend upon the relative magnitudes of DH₁, DH₂, and DH_H.

The heat of sublimation reflects the strength of metallic bonding in the solid state. However, the relationship between this bonding and ground-state electronic structure of a gaseous atom is very complex indeed. Be that as it may, uniform periodicity is clearly not observed; thus, ₃Li > ₁₁Na > ₁₉K (Group 1), but ₇₉Au > ₂₉Cu > ₄₇Ag (Group 11).

The 1st ionization energy is the only ergonic process which is directly related the ground-state electronic structure of a gaseous atom. Nevertheless, here also, uniform periodicity is not observed; thus, ₃Li > ₁₁Na > ₁₉K (Group 1), but ₇₉Au > ₂₉Cu > ₄₇Ag (Group 11).

The heat of hydration reflects the electronic structure of the gaseous cation and its subsequent bonding with a (variable) number of water molecules to form the hydrated cation. Unfortunately, a clear statement of periodicity is precluded because, in contrast to those in Group 1, the metals in Group 11 show variable oxidation states.

And finally, ... These data would support this principle: 'high metal reactivity is favored by a low heat of sublimation, a low ionization energy, and a high heat of hydration of the metal cation'. The overall heat energy change (DH) is negative for each Group 1 metal, and the relative magnitudes of DH parallel the measured energy changes of their reactions with water (i.e., Li > K > Na); the 'anomalous' position of lithium is attributable to the higher heat of hydration of the lithium cation. In contrast, largely because of silver's much higher ionization energy, DH is positive for this Group 11 metal; this is consistent with the observed lack of reaction between silver and dilute acid or water.

[Scene. A court in the state capital of Poppermania.] Mermaid: Plus horreur! ... M'Lud ... [The judge holds up his hand.] Judge: My Lord is the correct method of address, if you please. Mermaid: Sorry, my Lord. These results and explanations are all well and good: but they can have little relevance to solid ionic compounds, such as chlorides, oxides and nitrides, surely? Judge: [He smiles tolerantly at this less-than-humble student.] I do admit, strictly speaking, only parts are; for example, the DH1 and DH2 terms. However, for other reactants, there should be analogous terms to DHH and DHR. Perhaps you would care to note the relationship of DHH to the lattice energy? Mermaid: Duly noted, M'Lud ... I mean, my Lord. Please no more ... My time is valuable! [She states petulantly before glancing briefly, but proudly, at her varnished finger-nails.] Judge: Oh dear, in my day ... no, never mind. [He sighs.] Remember, Rome was not built in a day: although it may well have burnt down in one! [He glances at his fiddle before dabbing some eau-de-cologne on his pristine wig.] Mermaid, I ... advise you to spend at least part of your free-time giving the gray cells some aerobic exercise. [Sighs of relief from the rest of the synchronized-swimming team in the public gallery.] Mermaid: My Lord, perhaps I should emigrate to Laputa? [... but the venerable judge has fallen asleep (bless his silken sox).]

* The student is encouraged, albeit gently, to consider testing this hypothesis, or a similar one which focuses on Periods, using different physical data (e.g., heats of sublimation, ionization energies, energy changes for the formation of solid ionic compounds, ...); such data should be abstracted from reference books.